„Az egyetlen dolog ami alapján döntesz, az a piac viselkedése legyen!”
Leonardo Fibonacci
Fibonacci, más néven Leonardo di Pisa vagy Leonardo Fibonacci (kb. 1170 – kb. 1250) híres olasz matematikus volt, sokan a középkor legtehetségesebb nyugati matematikusának tartják, aki észrevett egy nagyon fontos számkombinációt. A sorozat képzése nem túl bonyolult, ám annál érdekesebb. A számok meghatározása úgy történik, hogy az első tagot 1-nek vesszük, majd ezt követően a sorozat következő tagját az azt megelőző két szám összegeként kapjuk. A sorozat tagjai így a következők lesznek:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, stb.
A Fibonacci számok és arányosságok elterjedt és közkedvelt eszközzé váltak a technikai elemzésben is. Könnyen és egyszerűen használhatóak, és leginkább egyértelmű támasz és ellenállási szinteket jelölnek ki a tréderek számára.
Aranymetszés
Az aranymetszés (phi) vagy aranyarány olyan arányosság, amely a természetben és a művészetben is gyakran megjelenik, természetes egyensúlyt teremtve a szimmetria és az aszimmetria között. A phi mindenütt jelen van a természetben, ami nem lehet véletlen, ezért tekintették az ókoriak a phi-t a világegyetem teremtője által megszabott számnak. A régen élt tudósok isteni arányszámnak vagy aranymetszésnek nevezték.
Fibonacci arányszámok
A Fibonacci sorozat kapcsolatban van az aranymetszéssel. A sorozat egyre nagyobb sorszámú elemeinek hányadosa egy állandó számhoz, az aranymetszéssel kapott hosszabbik szakasznak a rövidebbikhez való arányához közelít, a 0.618-hoz. A 34:55 osztása után az arányszám már nem változik.
Ha a sorozatban lévő nagyobb számot osztjuk a kisebbel, akkor a hányados az 1.1618 felé konvergál.
| Tagok és összegük | Tag és előző tag | Hányados |
|---|---|---|
| 1 + 1 = 2 | 1 : 2 | 0.500 |
| 1 + 2 = 3 | 2 : 3 | 0.667 |
| 2 + 3 = 5 | 3 : 5 | 0.600 |
| 3 + 5 = 8 | 5 : 8 | 0.625 |
| 5 + 8 = 13 | 8 : 13 | 0.615 |
| 8 + 13 = 21 | 13 : 21 | 0.619 |
| 13 + 21 = 34 | 21 : 34 | 0.617 |
| 21 + 34 = 55 | 34 : 55 | 0.618 |
| 34 + 55 = 89 | 55 : 89 | 0.618 |
Ezek a számok láthatóan vagy láthatatlanul, de működnek a világunkban, amelynek mi, emberek is a részei vagyunk, és mivel a mi döntéseink határozzák meg a piaci mozgásokat, a Fibonacci számok a piacon is életre keltek, és tudatosan vagy tudattalanul, de befolyásolják a kereskedői magatartást.
A Fibonacci számok tőzsdei használata
A Fibonacci számokkal kapcsolatban több eszközt találsz a kereskedési platformokban, így a MetaTraderben is:
E módszerek közül a leginkább elterjedt és a legnagyobb népszerűségnek örvendő a Fibonacci visszatérés, melyet a korrekció meghatározására, stop-loss, belépési és célár szintként is lehet használni, illetve a Fibonacci tágulás, amely a célár megállapítására lehet a segítségünkre. A Fibonacci arányok az Elliott hullámelmélet gyakorlati alkamazásában is fontos szerepet kapnak.
A technikaielemzésben használt fontosabb arányszámok:
0%, 23.6%, 38.2%, 50%, 61.8%, 100%,138.2, 161.8%, 200.0%, 261.8%, 423.6%
Fibonacci retracement (visszatérés)
A Fibonacci számokat – arányosságot – a forexben is használják támasz-ellenállás, célár és főleg visszatesztelési szintek meghatározásához. Az egyik legelterjedtebb használata a Fibonacci retracement, azaz Fibonacci visszatérés. A Fibonacci korrekcios számsor meghatározásánál a teljes korrekciót 100%-nak véve alapul, a megelőző Fibonacci számokat úgy kapjuk, hogy elosztjuk 1,618-al.
| 100% / 1,618 | 61,8% |
| 61,8% / 1,618 | 38,2% |
| 38,2% / 1,618 | 23,6% |
Amint látható: 23,6 + 38,2 = 61,8 továbbá 38,2 + 61,8 = 100.
Az emelkedés 100%-át osztva 1,618-al 61,8-at kapunk, tehát ez lesz az alapvető korrekciós szám, és így tovább.
Fibonacci korrekciós szintek a gyakorlatban
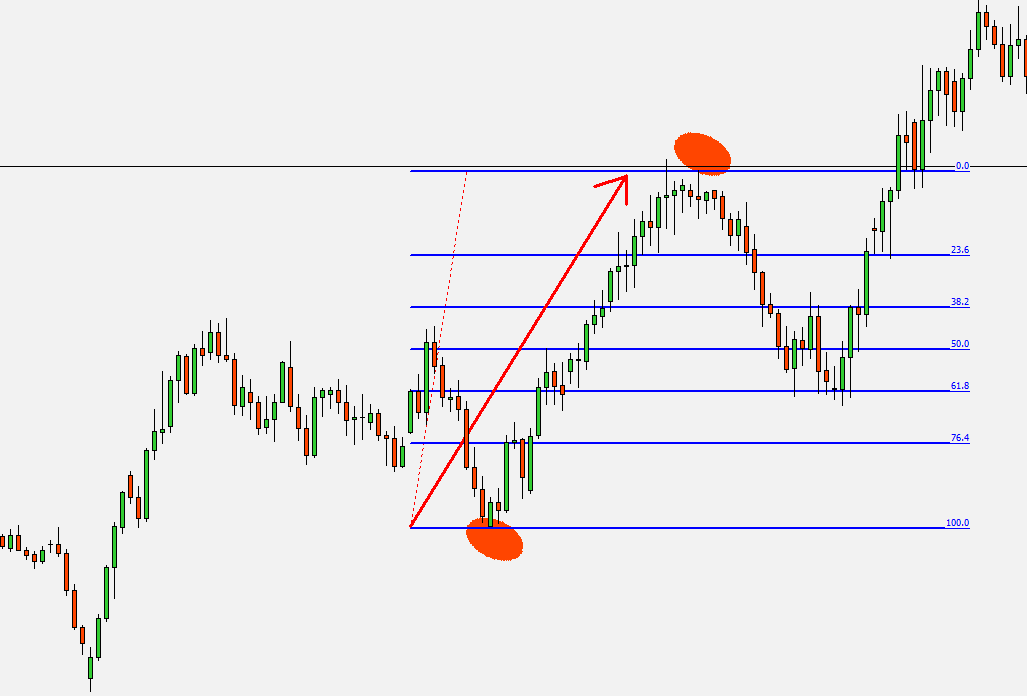
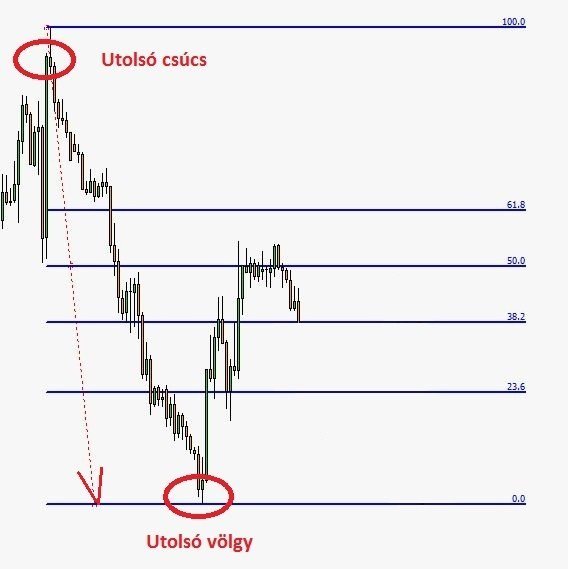
A Fibonacci korrekciós szintek megrajzolását azzal kezdjük, hogy húzunk egy vonalat a legutóbbi csúcs és völgy között – a gyertyák kanócához. A vonalak egy része nem lesz látható (tágulás), mivel azok a skálán kívülre esnek.
Emelkedő trendben
húzott Fibonacci szintek
Ezek a szintek viselkedhetnek a korrekcióban támaszként.
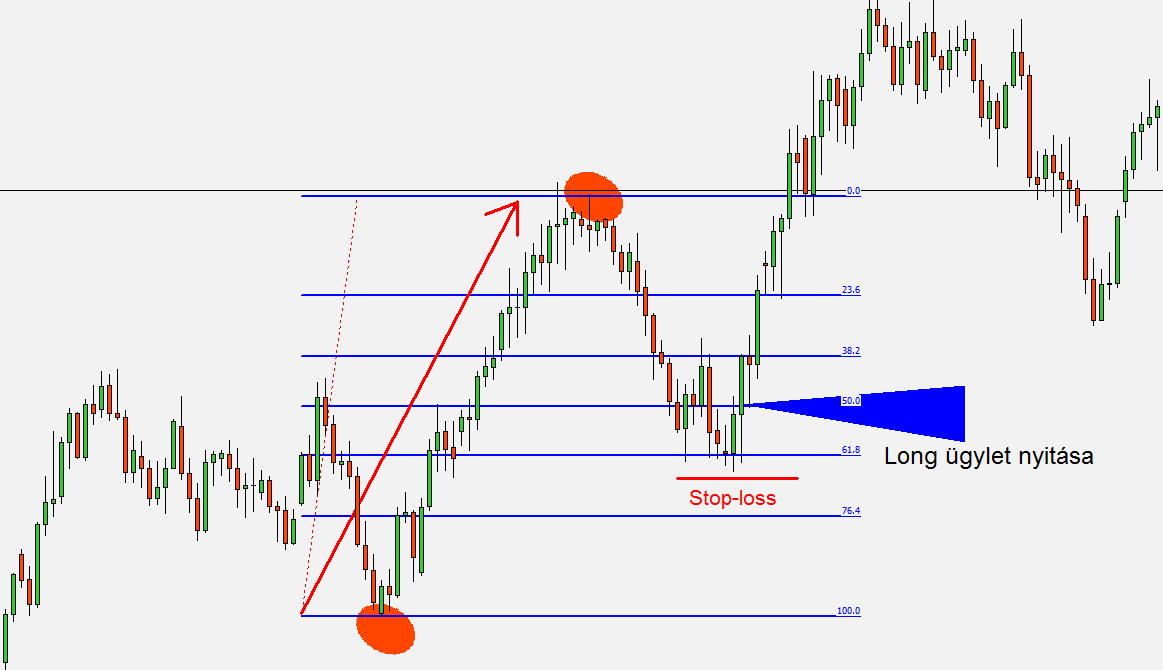
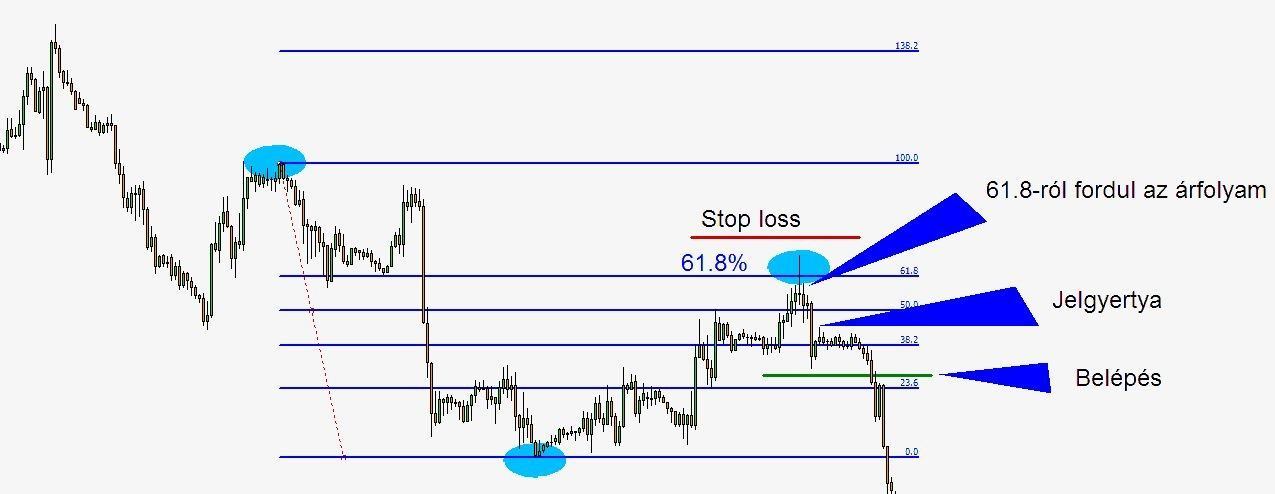
Ha emelkedő trendben korrekció történik (átmenetileg esik az árfolyam), számos esetben megfigyelhető, hogy a 38.2%, 50.0% vagy a 61.8%-ig korrigál vissza az ármozgás, majd folytatja a trend irányba az útját. Az árfolyam fordulása azért is történik ezekről a szintekről, mert sok kereskedő ide teszi a célárat – zárja a pozíciót, mások pedig ezeknek a szinteknek az elérésekor nyitnak ügyleteket a főtrend irányában.
Csökkenő trendben
húzott Fibonacci szintek
Ezek a szintek viselkedhetnek támasz és ellenállásként.
Ha csökkenő trendben korrekció történik, számos esetben megfigyelhető, hogy a 38.2%, 50.0% vagy a 61.8%-ig korrigál vissza az árfolyam, majd folytatja a trend irányba az útját. Az árfolyam fordulása azért is történik ezekről a szintekről, mert sok kereskedő ide teszi a célárat – zárja a pozíciót, mások pedig ezeknek a szinteknek az elérésekor nyitnak ügyleteket a főtrend irányában.
A legerősebb korrekciós szintek a 38,2%, 50,0%, 61,8%. Ha 23.6%-os szinten mutat megtorpanást az árfolyam, az még gyenge jelzés a fordulatra, és leginkább oldalazásra vagy rövid megtorpanásra utalhat – persze lehetnek esetek, amikor valóban megfordul a mozgás.
Egy trenden belül egyetlen hullámhoz, csúcshoz vagy mélyponthoz is behúzhatók a Fibonacci szintek annak megállapítására, hogy korrekció történik, vagy trend elbizonytalanodás.
A Fibonacci szintek áttörése jelzés lehet arra, hogy az árfolyam megindul a kitörés irányába, illetve ha fordul vagy pattan valamelyik vonaláról, az fordulatot vetíthet előre, azaz valószínűsíti a korrekció végét, és hogy az ármozgás visszatér a főtrend irányába.
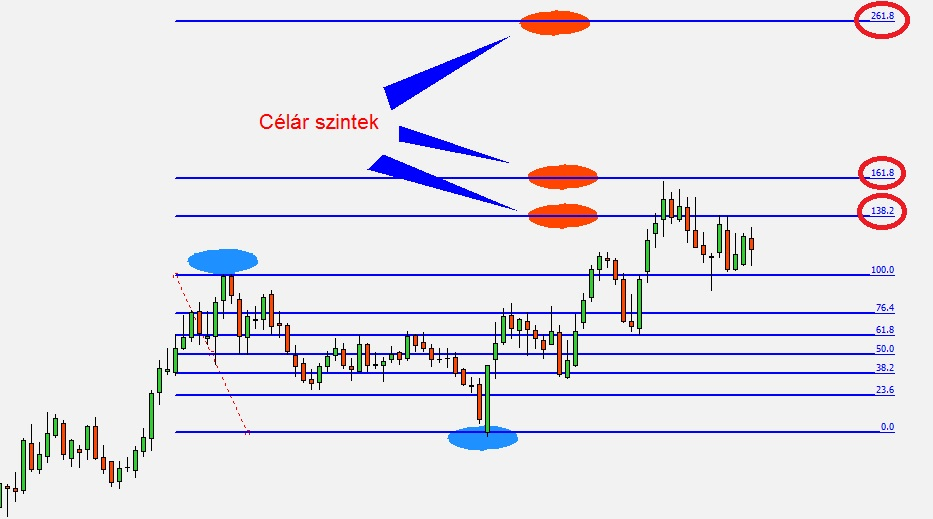
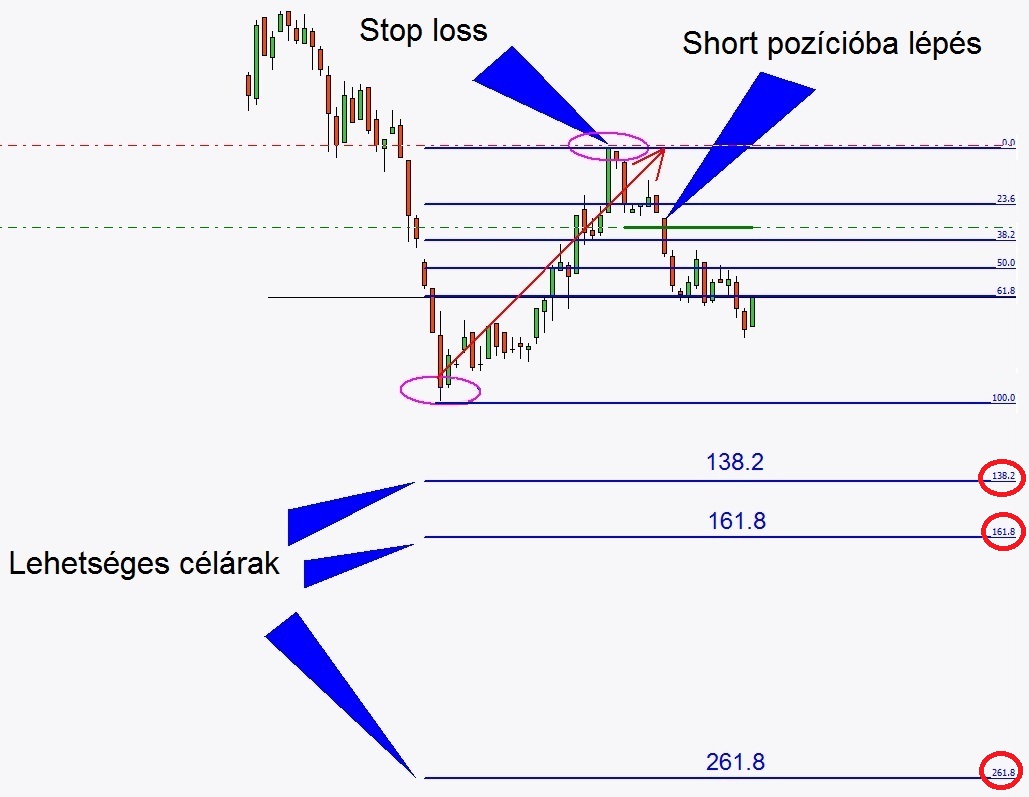
Fibonacci célár meghatározás
A Fibonacci szinteket követő stratégiában a célárakat is meghatározhatjuk a Fibo eszközzel, azaz a Fibonacci tágulással.
Példa emelkedő trendben
Amikor a lehetséges célárat keressük, akkor pont fordítva járunk el, mint amikor a korrekciós szinteket vizsgáljuk. Itt az eszközt a legutolsó csúcstól húzzuk lefelé a völgyhöz – ahonnan a fordulat feltételezhető.
Célár szintek lehetnek: 100.0%, 138.,%, 161.8%, 261.8%
Példa csökkenő trendben
Itt az eszközt a legutolsó aljtól húzzuk felfelé, a csúcsponthoz – ahonnan a fordulat feltételezhető. Itt is a gyertyák testéhez húzzuk a Fibonacci két végpontját.
Célár szintek lehetnek: 100.0%,138.2%, 161.8%, 261.8%
Szeretnéd jobban megismerni a technikai elemzés eszköztárát?
Remek kezdet lehet számodra A technikai elemzés és pénzkezelés PDF oktatóanyagunk.
Szeretnél hasonló tartalmakat kapni?
Iratkozz fel a Trader Klub hírlevelére!
Szeretnéd elsajátítani a kereskedés és piacelemzés képességét?
Ha érdekel a technikai elemzés, és szeretnél elsajátítani egy nyereségesen működtethető szabályrendszert, akkor a figyelmedbe ajánljuk a Szörf Mini Kereskedési Stratégiát, továbbá a Tőzsdeklubot, ahol láthatod és begyakorolhatod a rendszer alkalmazását.
Tetszett ez a cikk? Oszd meg, hogy másokhoz is eljuthasson!
Kapcsolódó bejegyzések
A szerzőről: Horváth Gábor
